Deep Learning in Forth
Part I

August 28, 2021

Brad Nelson / @flagxor

Overview

• Machine Learning is EXCITING!
• Why are neural networks "suddenly" working?
• Forth has a role to play!!!
• Introduce core Deep Learning
• Build a performant foundation in Forth
• More Next Time!

Caveat

https://commons.wikimedia.org/wiki/File:Alphago_logo_Reversed.svg

• Monte-Carlo tree search guided by policy and value networks
• Bootstrapped from studying human games
• Quickly defeats human players
  • Oct 2015 - 5:0 against Fan Hui (professional player)
  • Mar 2016 - 4:1 against Lee Sedol
  • May 2017 - 60:0 against professional including Ke Jie (#1 player)
• 2017 - AlphaGo Zero, bootstraped from scratch, single computer with 4 TPUs

StyleGAN (2019)

DALE-E (2021)

"an armchair in the shape of an avocado." ----- "a snail made of a harp." -----

https://daleonai.com/dalle-5-mins

Deep Nostalgia (2021)

AI Dungeon - GPT-3 (2021)

Github Copilot - GPT-3 (2021)

Why is this suddenly working?

• Core idea from 1986 (Backpropagation), why now?
• LOTS more compute
  • Moore's Law
  • GPUs & TPUs
  • Cloud Computing
• LOTS more data
  • Digital Cameras
  • Solid State Storage
  • The Internet
• Better techniques & fixed early mistakes

Where does Forth fit in?

• Deep Learning involves powerful,
  but SIMPLE ideas
• Interactivity is important, not high-level performance (Python is the dominant language)
• Small ML models fit in embedded devices
• Big new things shift what's important

Deep Learning in a Nutshell

• AI, Neurons, Aritificial Neurons, and Perceptrons
• Layers as Matrices (and Tensors)
• How "Deep" Learning Works
• Crucial details for making it work well

Approaches to AI

• Symbolic
  • Popular initially
  • Appealing because of Platonic ideal of knowledge
  • Tractable because of limitations of early computers
• Connectionist
  • Now very hot
  • Appealing because it appears to mirror the brain
  • Also appealing because it offers a model for "learning"
  • Downside: "unexplainable" systems

Neurons

• Firing frequency varies by stimulus
• Learning mechanism poorly understood

Artificial Neurons

• Mathematical / Engineering construct, inspired by biology
• Variations in layering and activation function

Matrix Representation

• Each layer is a matrix multiply with activation applied to each element

Network Layers

• Input/Ouput + zero or more "hidden" layers
• Multiple layers required for complex functions

Perceptron - 1958

• Hardware Artificial Neural Network
• Single Layer (Linear Planes)

Improvements + Advances

• Automatic Differentiation
• Better Initialization
• Better Activation Functions
• Better Layers
• Better Overall Structure

How to Learn

• Tune the network so that training input → output values produce the expected results
• Treat the whole network as a function F, and minimize Loss(F(input), expected)
• Use a "loss function", like sum of squares or distance sum

How to Learn

• Gradient Descent on weights and biases
• Move "downhill" in n-dimensions
• Need to be able to differentiate whole neural network + loss function

Ways to find a Derivative

• Symbolic Differentiation
• Numeric Differentiation
• Automatic Differentiation

Automatic Differentiation

• Compute the function for particular input
• Use intermediate results with chain rule to find derivative at that same input point
• Two approaches (for function for ℝⁿ → ℝ^m)
  • Forward Accumulation (better if n << m)
  • Reverse Accumulation (better if n >> m)
• Minimizes round-off error

Chain Rule

Multivariable Chain Rule

Forward Accumulation

Reverse Accumulation

AutoDiff with Matrices

• Reverse Accumulation generalizes to matrices!
• Product rule works as you would expect
• Per-element operations also generalize

Initialization

• Biases - zero
• Random weights to balance variance between layers.

Activation Functions

\[ tanh(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}} \]
\[ logistic(x) = \frac{1}{1 + e^{-x}} \]
\[ relu(x) = max(0, x) \]

Convolutional Neural Networks

• Image recognition of low level features should be the same throughout the visual field
• Why relearn it over and over?
• Apply the same windowed network throughout the image!

Discrete Convolution

2D Discrete Convolution

2D Discrete Convolution

Identity
Edge Detection
Gaussian Blur

Convolutional Filters

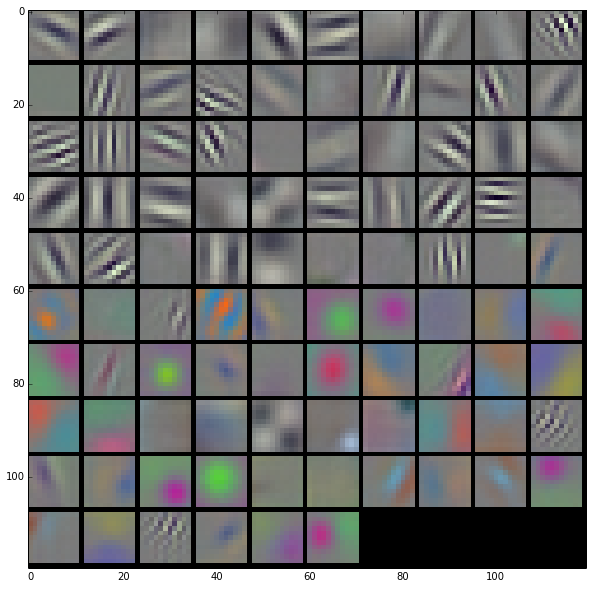
Other Structures

• Generative Adversarial Networks
• Recurrent Neural Networks
• Transformer Recurrent Neural Networks

Pivot to Performance

• We are doing LOTS of matrix operations!
• Matrix multiply will dominate, it's O(n³) when done naively
• Strassen's algorithm is O(n^log₂7) ≈ O(n^2.807)
• Best theoretical as of 2020 is O(n^2.3728596), but has "galactic" constants
• How to best use the hardware?

BLAS

Basic Linear Algebra Subprograms

• FORTRAN Library
• Terse ≤6 character names
• Standard "Kernels"
• Strided Data

Strided Data

Type Convensions

• S = Single precision (32-bit) floats
• D = Double precision (64-bit) floats
• C = Single precision complex (2 x 32-bit) floats
• Z = Double precision complex (2 x 64-bit) floats

BLAS - Level 1 (1979)

• *ROTG + SROT - Givens rotation
• *SWAP - Swap two vectors
• *SCAL - Vector scaling x = a*x
• *COPY - Vector copy
• *AXPY - Vector scale and add y = a*x + y
• *DOT - Dot product
• *NRM2 - Euclidean norm / vector length
• *ASUM - Vector sum of absolute values
• I*AMAX - Index of max absolute value

BLAS - Level 2 (1984-88)

• *GEMV - Matrix Vector Multiply \[ y := \alpha A x + \beta y \]
• *GER - Row-column Vector multiply \[ A := \alpha x y^T + A \]
• Matrix-vector operations on symmetric/triangular matrices stored in banded or packed format.
• Transpose generously supported.

BLAS - Level 3 (1990)

• *GEMM - Matrix Matrix Multiply \[ C := \alpha A B + \beta C \]
• Matrix-matrix operations on symmetric/triangular matrices stored in banded or packed format.
• Transpose generously supported.

SAXPY

       SUBROUTINE saxpy(N,SA,SX,INCX,SY,INCY)
       REAL SA
       INTEGER INCX,INCY,N
       REAL SX(*),SY(*)
       INTEGER I,IX,IY,M,MP1
       INTRINSIC mod
 
       IF (n.LE.0) RETURN
       IF (sa.EQ.0.0) RETURN
       IF (incx.EQ.1 .AND. incy.EQ.1) THEN
          m = mod(n,4)
          IF (m.NE.0) THEN
             DO i = 1,m
                sy(i) = sy(i) + sa*sx(i)
             END DO
          END IF
          IF (n.LT.4) RETURN
          mp1 = m + 1
          DO i = mp1,n,4
             sy(i) = sy(i) + sa*sx(i)
             sy(i+1) = sy(i+1) + sa*sx(i+1)
             sy(i+2) = sy(i+2) + sa*sx(i+2)
             sy(i+3) = sy(i+3) + sa*sx(i+3)
          END DO
       ELSE
          ix = 1
          iy = 1
          IF (incx.LT.0) ix = (-n+1)*incx + 1
          IF (incy.LT.0) iy = (-n+1)*incy + 1
          DO i = 1,n
           sy(iy) = sy(iy) + sa*sx(ix)
           ix = ix + incx
           iy = iy + incy
          END DO
       END IF
       RETURN
       END
					

Utilities

1 sfloats constant sfloat
1 dfloats constant dfloat
variable incx   sfloat incx !
variable incy   sfloat incy !

: sf, ( r -- ) here sf! sfloat allot ;
: df, ( r -- ) here df! dfloat allot ;

: sxsy+ ( sx sy -- sx' sy' ) incy @ + swap incx @ + swap ;
					

SAXPY

: saxpy ( sx sy n f: sa -- )
  0 ?do over
    sf@ fover f* dup sf@ f+ dup sf! sxsy+
  loop 2drop fdrop ;
					

Basic Ops

: sswap ( sx sy n -- )
   0 ?do dup sf@ over sf@ dup sf! over sf! sxsy+ loop 2drop ;

: sscal ( sx n f: sa -- )
  0 ?do dup sf@ fover f* dup sf! incx @ + loop drop fdrop ;

: scopy ( sx sy n -- )
  0 ?do over sf@ dup sf! sxsy+ loop 2drop ;
					

SDOT

: sdsdot ( sx sy n f: sb -- f: prod )
  0 ?do over sf@ dup sf@ f* f+ sxsy+ loop 2drop ;
: sdot ( sx sy n -- f: prod ) 0e sdsdot ;
: dsdot ( sx sy n -- f: prod ) 0e sdsdot ;
					

Summing and Searching

: snrm2 ( sx n -- f: norm )
  0e 0 ?do dup sf@ fdup f* f+ incx @ + loop drop fsqrt ;

: sasum ( sx n -- f: abssum )
  0e 0 ?do dup sf@ fabs f+ incx @ + loop drop ;

: isamax ( sx n -- index )
  over sf@ fabs 0 -rot 0 ?do
    dup sf@ fabs fover f> if fdrop dup sf@ fabs nip i swap then
    incx @ +
  loop drop fdrop ;
					

Givens Rotation

Givens Rotation

fvariable cos
fvariable sin

: srotg ( f: a b -- f: c s )
  fdup f0= if fdrop fdrop 1e 0e exit then
  fover fover fdup f* fswap fdup f* f+ fsqrt 1/f ( a b 1/h )
  frot fdup f0<= if fswap fnegate fswap then ( b ~1/h a )
  fover f* frot frot f* ;

: srot ( sx sy n -- )
  0 ?do over sf@ cos sf@ f* dup sf@ sin sf@ f* f+
        dup sf@ cos sf@ f* over sf@ sin sf@ f* f-
        dup sf! over sf! incy @ + swap incx @ + swap loop 2drop ;
					

Cblas

• C wrapper around F77 BLAS
• Cleverly works around Row vs Column major order

 void cblas_saxpy(const int N, const float alpha,
                  const float *X, const int incX,
                  float *Y, const int incY);
					

Row-Major vs Column-Major Order

• FORTRAN = Column-Major Order
• C = Row-Major Order
• Forth = \o/ No arrays,
  I do what I want!
• Transpose parameters
  allow conversion

Cblas

: sfcell/ ( n -- n ) 2/ 2/ ;

c-function cblas_dsdot cblas_dsdot n a n a n -- r
: dsdot ( sx sy n -- f: prod )
  -rot >r incx @ sfcell/ r> incy @ sfcell/ cblas_dsdot ;

c-function cblas_saxpy cblas_saxpy n r a n a n -- void
: saxpy ( sx sy n f: sa -- )
  -rot >r incx @ sfcell/ r> incy @ sfcell/ cblas_saxpy ;
					

SAXPY / DAXPY - Level 1 Benchmark

• 1000x - Multiply and Adds of two 1M element vectors
• Try both single and double precision
• Compare Forth and BLAS
• Multiplies: 1 Billion
• Adds: 1 Billion
• BLAS Baseline: 0.454s

SAXPY / DAXPY - Level 1 Benchmark

1000000 constant test-size
1 sfloats incx ! 1 sfloats incy !

test-size sfloats allocate throw constant foo
foo test-size sfloats 33 fill
test-size sfloats allocate throw constant bar
bar test-size sfloats 33 fill
: benchmark
  1000 0 do
    123e foo bar test-size saxpy
  loop
;
benchmark
					

SGEMV - Level 2 Benchmark

• 10x - Vector-Matrix Multiply of size 10K x 10K
• Compare Forth and BLAS
• Compare Forth at Level 1+ vs Level 2 only
• Multiplies: 1.0002 Billion
• Adds: 1.0002 Billion
• BLAS Baseline: 1.200s

SGEMV - Level 2 Benchmark

10000 constant test-size
1 sfloats incx ! 1 sfloats incy !

test-size test-size * sfloats allocate throw constant mat
mat test-size test-size * sfloats 33 fill
test-size sfloats allocate throw constant vec
vec test-size sfloats 33 fill
test-size sfloats allocate throw constant vec2
vec2 test-size sfloats 33 fill
test-size sfloats lda !
: benchmark
  10 0 do
    9e 1e mat vec vec2 test-size test-size sgemv
  loop
;
benchmark
					

SGEMM - Level 3 Benchmark

• One 1000 x 1000 Multiply and Add
• Compare Forth and BLAS
• Compare Forth at Level 1+, Level 2+, and Level 3 only
• Multiplies: 1.002 Billion
• Adds: 1.002 Billion
• BLAS Baseline: 0.462s

SGEMM - Level 3 Benchmark

1000 constant test-size
1 sfloats incx ! 1 sfloats incy !
#NoTrans transa !
#NoTrans transb !

test-size test-size * sfloats allocate throw constant mat1
mat1 test-size test-size * sfloats 33 fill
test-size sfloats lda !
test-size test-size * sfloats allocate throw constant mat2
mat2 test-size test-size * sfloats 33 fill
test-size sfloats ldb !
test-size test-size * sfloats allocate throw constant mat3
mat3 test-size test-size * sfloats 33 fill
test-size sfloats ldc !

: benchmark
  9e 1e mat1 mat2 mat3 test-size test-size test-size sgemm
;
benchmark
					

Intel MKL

• Intel oneAPI Math Kernel Library
• Linux, Windows, and OSX Intel Optimized Math Kernels
• Structured to heavily focus on Intel over AMD
• Implements BLAS and other kernels like FFT
• Takes advantage of: threads, memory layout, SIMD, the works

Wall Clock - System BLAS vs MKL BLAS

GigaFLOPS - System BLAS vs MKL BLAS

Wall Clock - System BLAS vs MKL BLAS

GigaFLOPS - System BLAS vs MKL BLAS

Speed!

• MKL SGEMM is 1,512x faster than high level Forth!
• But the layers were Matrix x Vector?

Batches

How to do fast convolution?

• Using a custom kernel could work, but would require optimizing another core operation
• Can we transform our input so that matrix multiplication becomes convolution?

im2col

im2col

: im2col { src b w h c dst fw fh }
  w h * c * sfloats { sb }
  h c * sfloats { sw }
  c sfloats { sh }
  c fh * sfloats { shc }
  src dst
  b 0 do
    over swap
    w fw - 1+ 0 do
      over swap
      h fh - 1+ 0 do
        over swap
        fw 0 do
          2dup shc cmove
          shc + swap sw + swap
        loop
        nip
        swap sh + swap
      loop
      nip
      swap sw + swap
    loop
    nip
    swap sb + swap
  loop
  2drop
;
					

im2col'

: im2col-size { b w h c fw fh } b  w fw - 1+ *  h fh - 1+ *  c * ;
: im2col' { src b w h c dst fw fh }
  dst b w h c fw fh im2col-size 0 fill
  sfloat incx ! sfloat incy !
  w h * c * sfloats { sb }
  h c * sfloats { sw }
  c sfloats { sh }
  c fh * { shc# }
  shc# sfloats { shc }
  dst src
  b 0 do
    over swap
    w fw - 1+ 0 do
      over swap
      h fh - 1+ 0 do
        over swap
        fw 0 do
          2dup swap shc# 1e saxpy
          shc + swap sw + swap
        loop
        nip
        swap sh + swap
      loop
      nip
      swap sw + swap
    loop
    nip
    swap sb + swap
  loop
  2drop
;
				

im2col Performance

• ~1.8 sec for 1024 128x128x3 images
• ~7.6 sec for multiply
• NOTE: The resulting matrix can be reshaped into expected output in place

Tensors

• Many multidimensional tensors can be flattened to big matrices and correctly multiplied after adjusting shape
• This will let us batch many items together

Multiple Filters and Images

First Deep Learning Target Project

• Recognize handwritten digits
• Use a series of 3x3 convolution layers, followed by some dense layers
• Classify into 0-9

MNIST (1998)

• Handwritten digit dataset
• 28x28 grayscale
• 60,000 training images
• 10,000 test images
• Remixed of NIST high school student and census bureau datasets

IDX File Format

Big Endian

$00    - Magic #                            (byte)
$00    - Magic #                            (byte)
type   - $08=uint8 $09=int8 $0B=int16       (byte)
         $0C=int32 $0D=float32 $0E=float64
rank   - Number of dimensions               (byte)
dim 1  - Size in dimension 1                (int32)
....                                        ....
dim N  - Size in dimension N                (int32)
data   - Raw data
          

Convert to Float

: u8tof32 ( a a n -- )
  0 do
    over c@ s>f dup sf!
    1 sfloats + swap 1+ swap
  loop 2drop ;
					

Convert to Float

\c void u8tof32(const uint8_t *src, float *dst, size_t n) {
\c   for (;n;--n) {
\c     *dst++ = *src++;
\c   }
\c }
c-function u8tof32 u8tof32 a a n -- void
					

MNIST (1998)

Next Time

• Build Neural Network Layer Words
• Implicitly build a reverse pass to calculate the gradient
• Current Code tally: ~1,292 lines

flagxor.com
slides
code

⚘

Thank you